Five Dynamo list nodes

The following nodes were quite mysterious to me and I had never used them, preferring to fall back on C# code when list manipulations were becoming too complex. While I was working on a curriculum for teaching Dynamo, I had to look harder at them and realized how powerful they can be.

So here are five list nodes that I can’t live without by now

List.SortByKey
List.GroupByKey
List.MaximumItemByKey and List.MinimumItemByKey
List.Combine
Function.Compose

List.SortByKey

To understand this node, we need to explain the sortable notion. In Dynamo, only numbers and text are sortable elements. Its means that you can only sort list of numbers or texts. You can then use for example the List.Sort node to order these lists.

To sort any other type of element, you need to explain to Dynamo how to sort these elements. The List.SortByKey node is one these nodes.

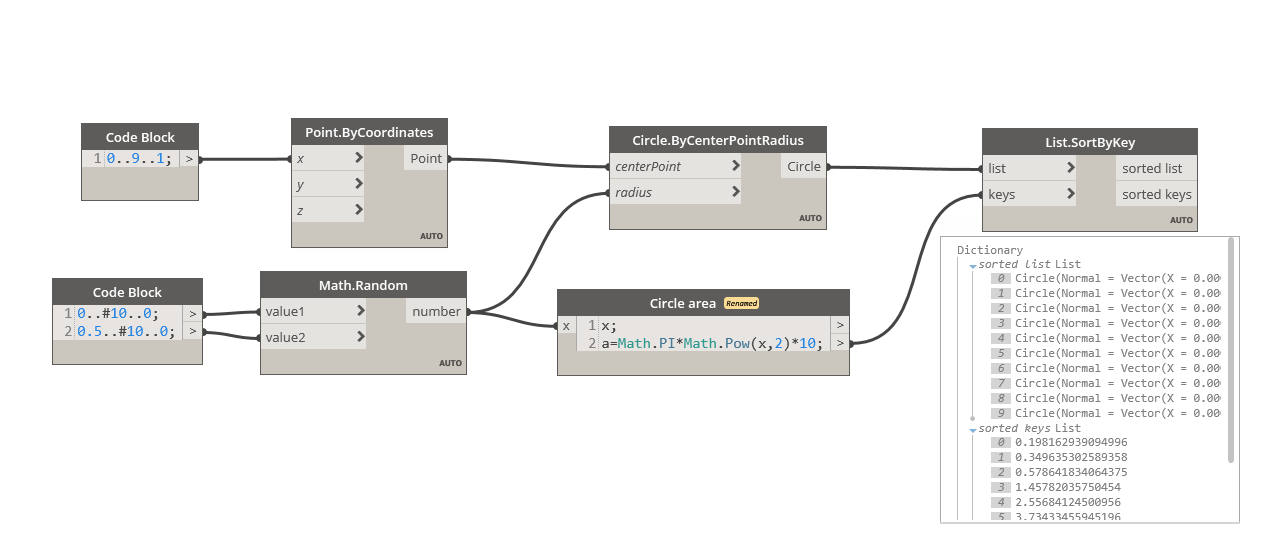
As an example, we use a list of 10 circles of random diameters that we want to sort by area (List 1). We then create a second list with the area of these circles (List 2). The second list contains number, it is a sortable list.

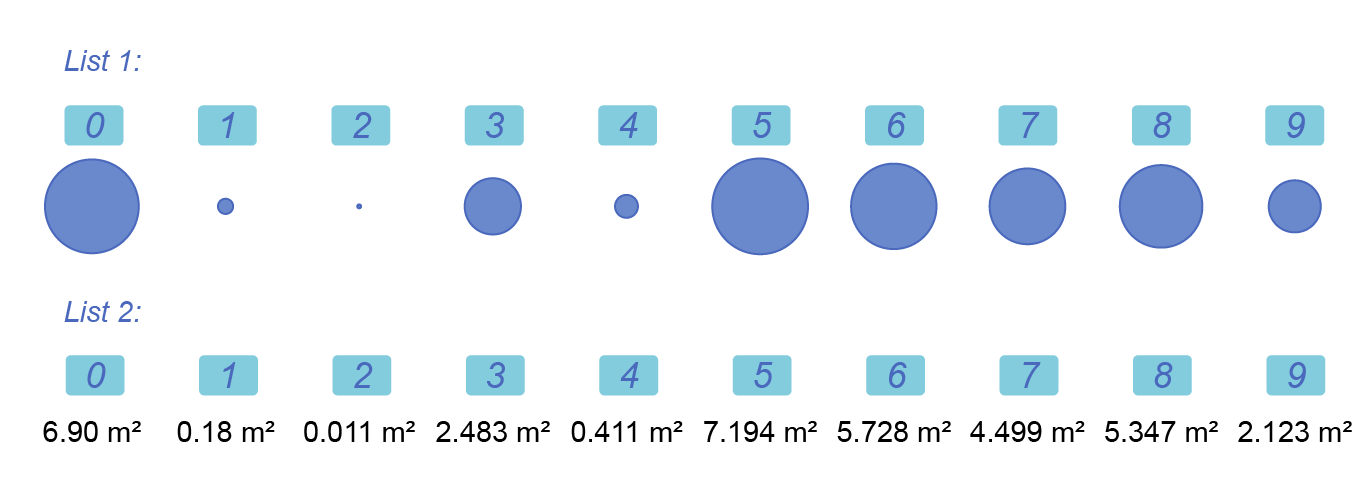
A list of circles and their area

The List.SortByKey will then sort the “keys” list and use the same order for the elements from the “list” list.

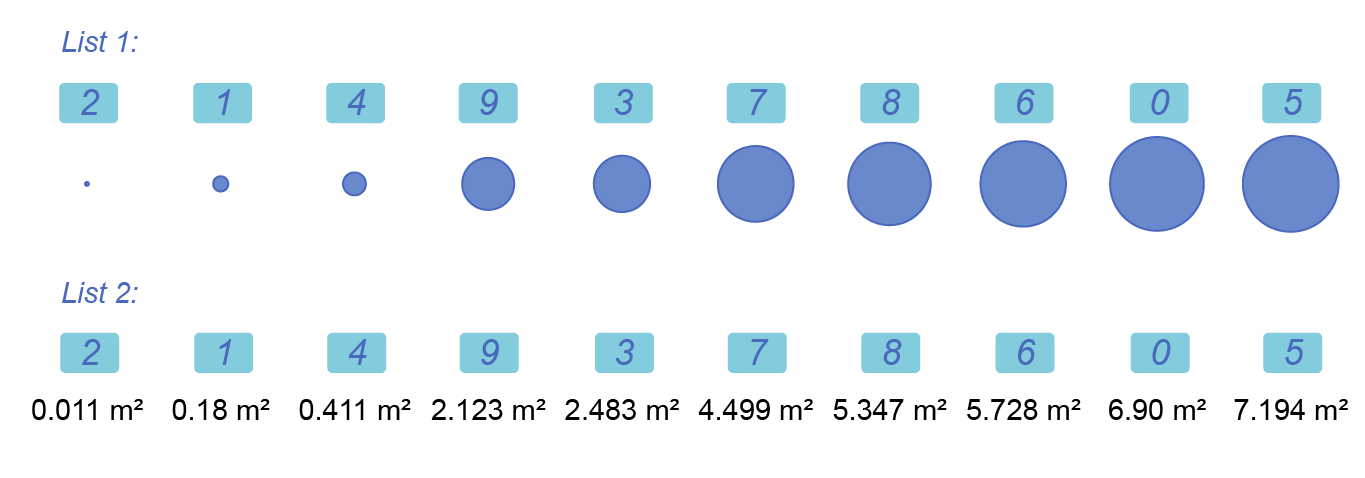
The sorted circles

We end up with two new lists. In the first one, we have the sorted elements from the “list” list, here the circles. In the second one, we have the sorted keys, the areas.

The resulting Dynamo definition

This allows us to sort our circles by area even if circles are not “sortable” by themselves.

List.GroupByKey

The List.GroupByKey node is a combination of List.SortByKey and List.GroupByEqual. You use it to regroup elements in sub lists.

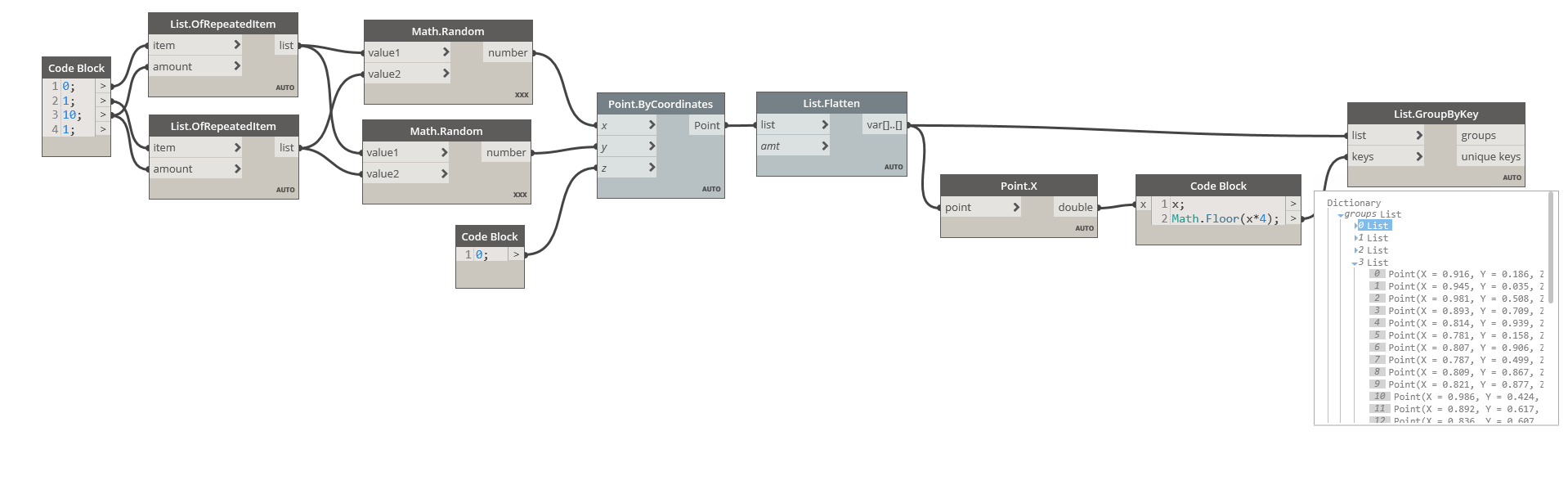
As an example, we use 16 points randomly scattered in a 1x1 square. These points are randomly positioned in a list.

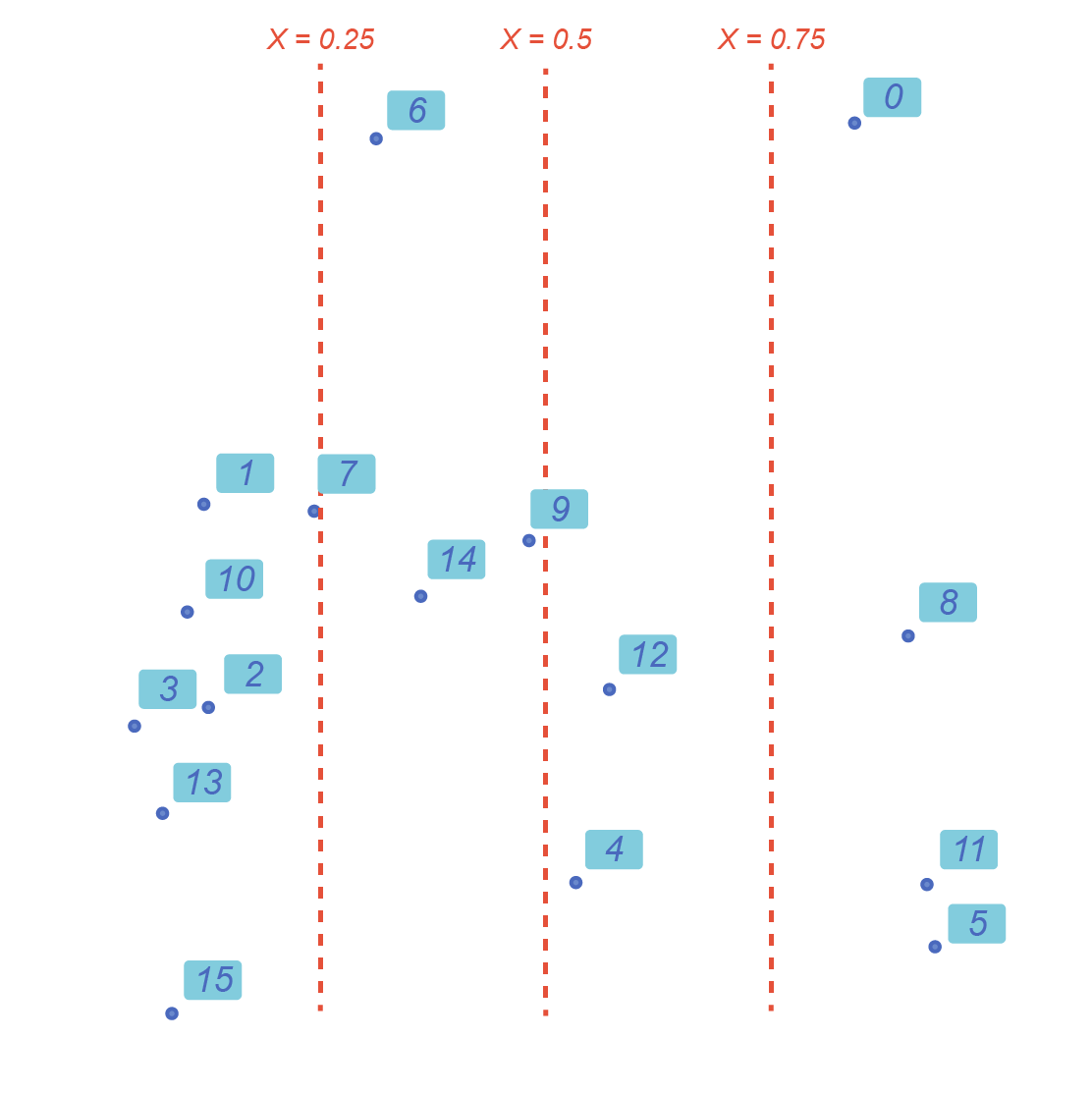
16 random points

We then create a list of number N indicating where the X coordinate of a point is located in the square :

If    0 < X < 0.25, N=0
If 0.25 < X < 0.5 , N=1
If  0.5 < X < 0.75, N=2
If 0.75 < X < 1   , N=3

The List.GroupByKey will then group all the equal keys together and use the resulting groups as a pattern to group the elements in the list.

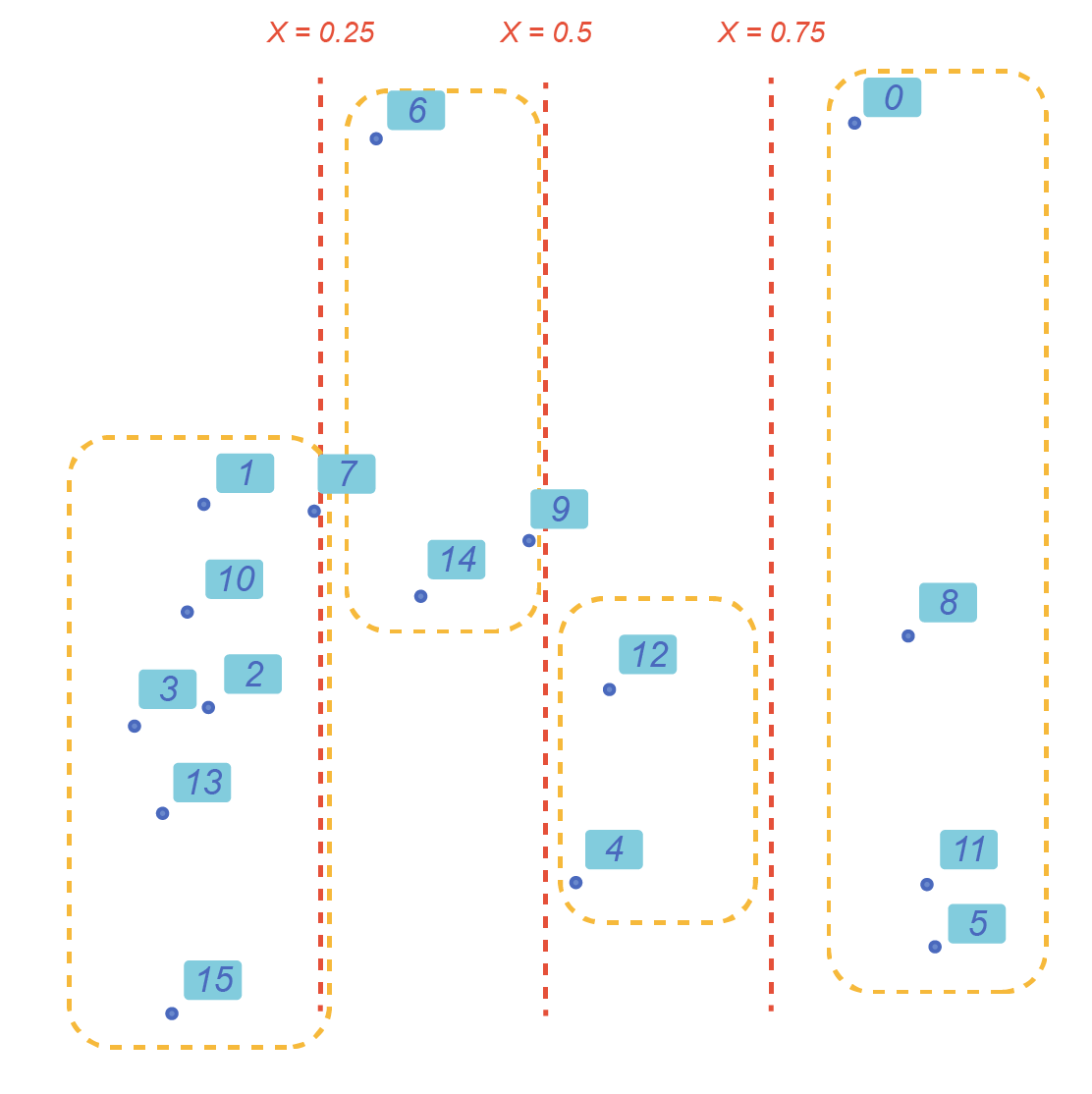
The points grouped by their position along the X axis

Here, we get four sub lists in the groups output, one for each group of X values. We also get the list of unique keys used to create the groups.

The resulting Dynamo definition

List.MaximumItemByKey and List.MinimumItemByKey

You can use these two nodes to find the “first” or “last” item in a list of non-sortable objects.

These nodes need a function input. Instead of providing a list of sortable keys like before, you provide the function (the “method”) to “explain” to the node how to sort the input elements. You will need to pass here a function object, so a node with an empty input ( i.e. leave some of the inputs blank).

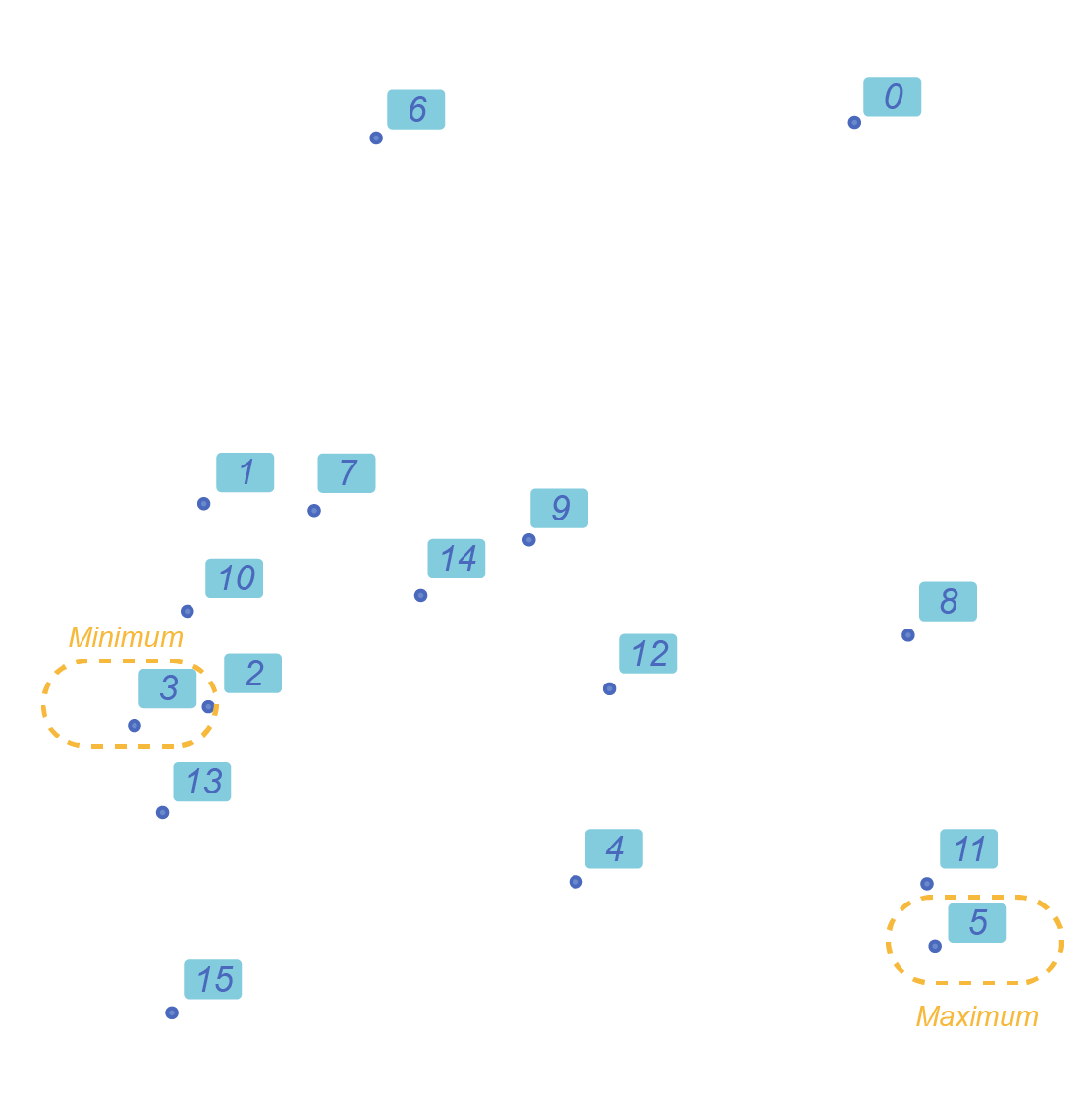
Here, we use again our list of random points and pass as keyProjector the Point.X node.

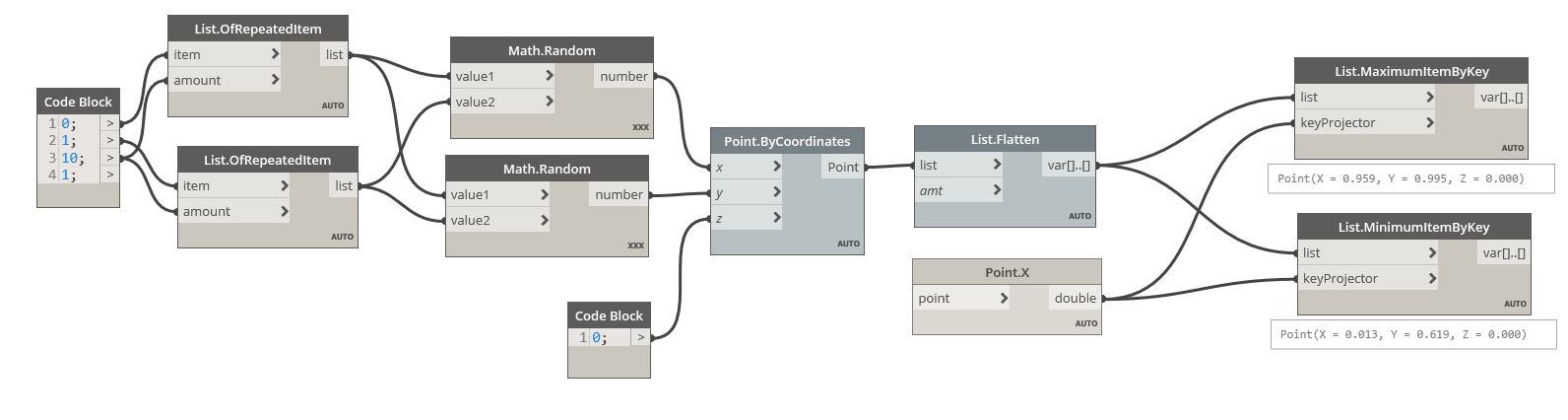
The Dynamo definition

This will « explain » to the List.MinimumKey node where to find the sortable value used to compute the minimum of the list.

The minimum and maximum points along the X axis

List.Combine

The List.Combine create a list combining two or more input list. The « method » used for combining these lists is described in the « comb » input, a function input.

To demonstrate how to use this node, let say I have a list of Pokémon names (are these still a thing?) that I want to concatenate with their type (yes, Pokémon too have a type).

Using the “String.Concat” node will not work, as the node concatenate each list and not each element of the list:

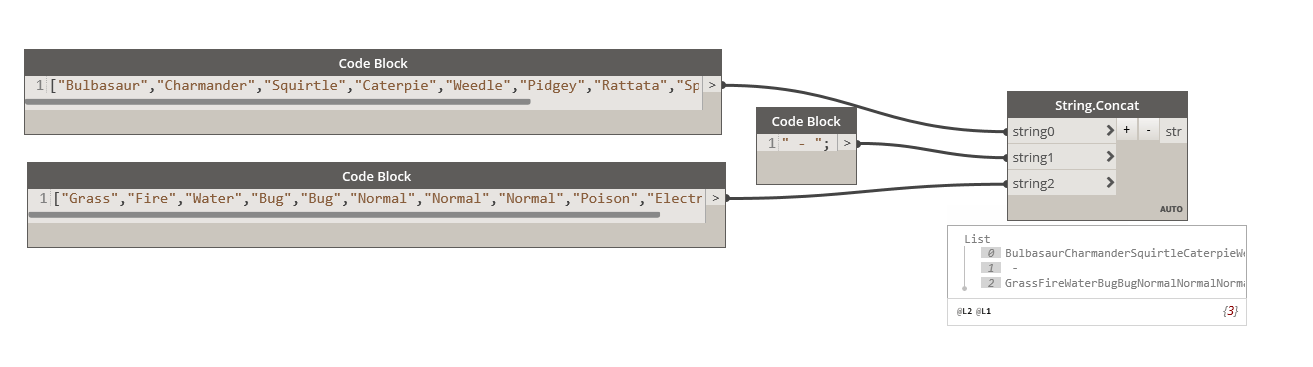
Using String.Concat directly

So we use the List.Combine to apply the function “String.Concat” to the two list, creating the expected result.

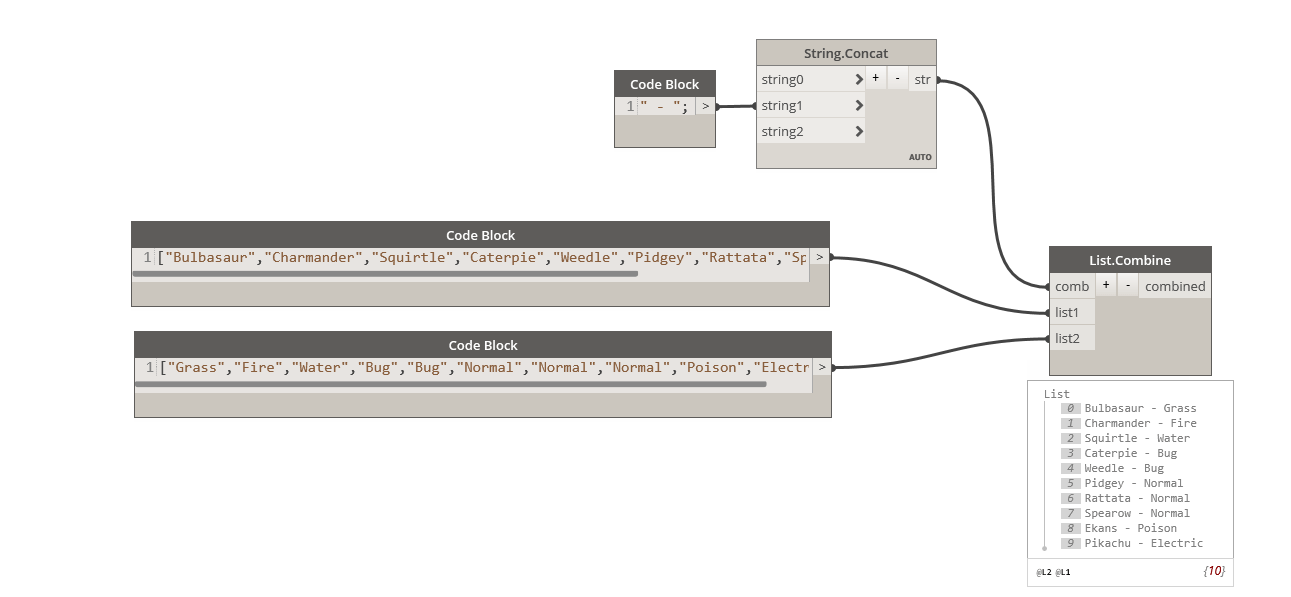
Using String.Concat through the List.Combine node

The two list must be of the same length, or the remain items in the longest list will produce null values. In case you want to combine your two lists with a different lacing method, the node List.LaceLongest, List.LaceShortest and List.Cartesian product will use the same principle but with different combinations.

Function.Compose

The “Function.Compose” is a bit special because it specifically expects a function object ( a node with some of the input left blank). This node will allow you to create a new function object combining multiple function node. You can then use this new function object in node such as List.Map, List.Combine, …. or any other node accepting a function object as input.

Each function is applied to the argument one after the other. You must take car of the type of input for each fuction:

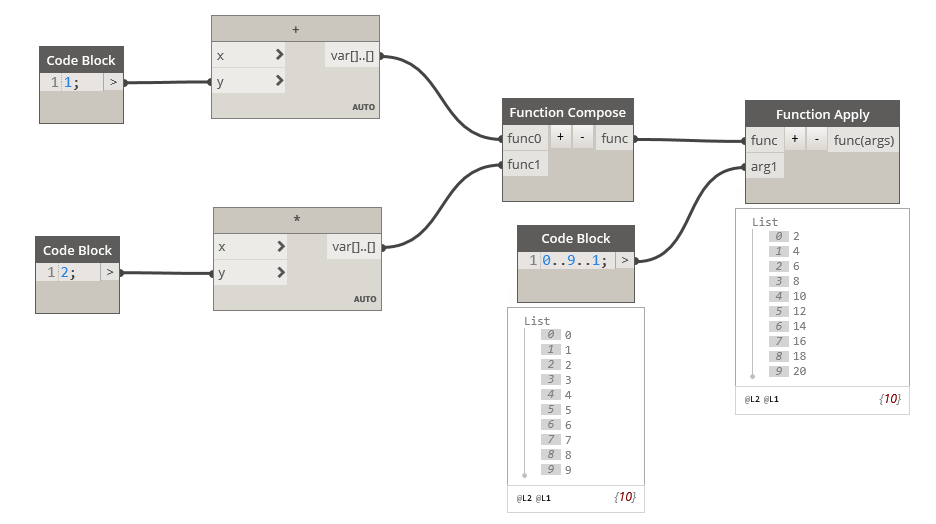
A very simple and useless Function.Compose example

You can use the Function.Compose node with Function.Apply (to apply the function to a given argument), but I found it much more useful with the List.Map node. The List.Map is not very useful by itself, since most of its functionality can be done with List@Level. But used with the List.Combine node, it allows powerful and compact graphs.

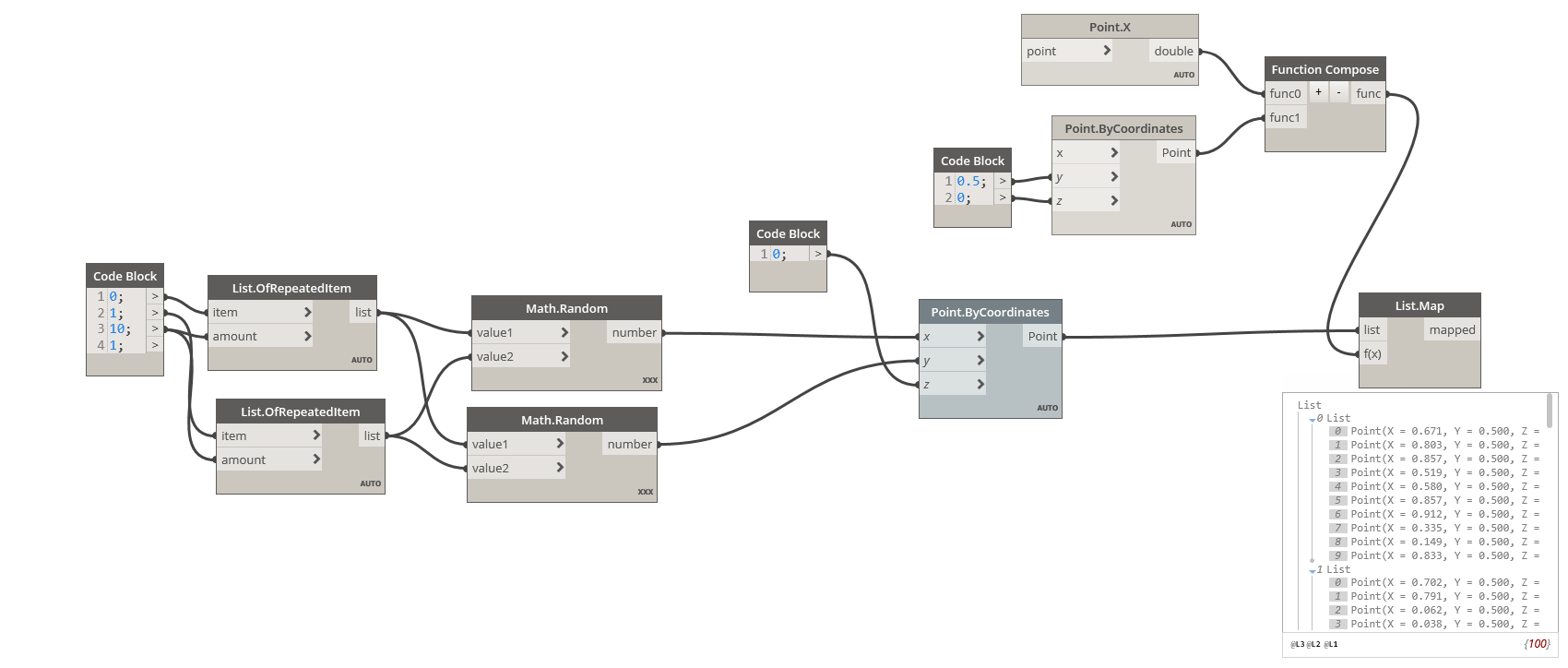
A more interresting example

With the function.Compose, you can create sophisticated series of operation and then apply them to all elements of your list

Of course, some of the functionality presented here can also be reproduced using List@Level, but I find these nodes to be much more legible and self-explanatory. They also illustrate how many paths can be taken to achieve the same goal in Dynamo. I hope you will find them as useful as me.